Step1-定义数据集

用于创建 ChatGPT 的数据集为 570 GB。假设数据集为一下内容：

白日依山尽，黄河入海流。
马无夜草不肥，人无横财不富。
天行健，君子以自强不息，地势坤，君子以厚德载物。

Step2-计算词汇量

Dataset 中单独单词的总数为词汇量。它可以通过一下公式计算，其中单独单词的总数为N：

为了找到N（总词数），将以上数据集分解为单个字。

在获取到N之后，执行集合操作以删除重复项，其中独特字的数量就是词汇量大小。

因此，词汇量大小为26，因为数据集中有26个单独的字。

Step3-Encoding编码

众所周知，神经网络做的是数学计算，它接收的是数字而非其他任何内容，所以这里我们需要为每一个字符分配一个唯一的数字。将单个Token视为一个字并为其分配一个数字：

Step4-计算Word Embedding

Encoding 完整个数据集后，现在选择我们的输入并开始使用 Transformer 架构工作。从语料库中选择一个句子马无夜草不肥在Transformer架构中处理：

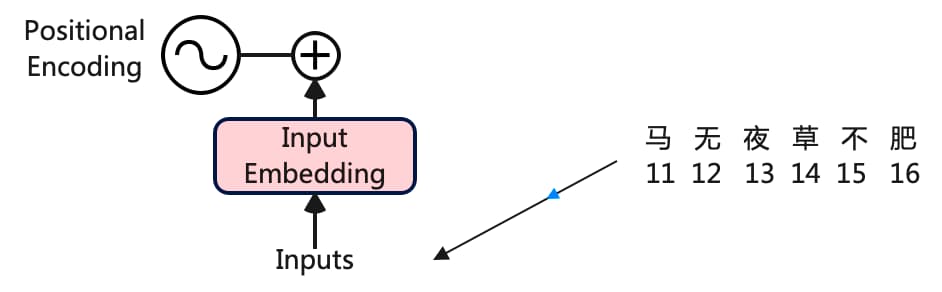
《Attention Is All You Need》论文中为每个输入词使用了512维的嵌入向量:

使用较小的嵌入向量维度来可视化计算的进行过程。因此，我们将使用嵌入向量的维度6。

这些嵌入向量的值介于 0 和 1 之间，先用随机数来填充一下矩阵。随着我们的 transformer 开始理解词语之间的含义，这些值随后会通过计算了更新。

Step5-计算Positional Embedding

根据嵌入向量中第 i 个值的每个词的位置，有两种计算位置嵌入Positional Embedding的公式：

我们的输入句子是“马无夜草不肥”，起始词是“马” ，起始索引（POS）值为 0，维度（d）为 6。对于 i 从 0 to 5 ，计算输入句子第一个词的位置嵌入Positional Embedding：

同样为输入句子马无夜草不肥中的所有字计算位置嵌入：

Step6-整合Word and Positional Embedding

这个由两个矩阵（词嵌入矩阵和位置嵌入矩阵）组合而成的结果矩阵将被视为编码部分的输入。

Step7-多头注意力

多头注意力由许多单头注意力组成，需要组合多少个单头注意力取决于我们。例如，Meta 的 LLaMA LLM 在编码器架构中使用了 32 个单头注意力。以下是单头注意力外观的示意图：

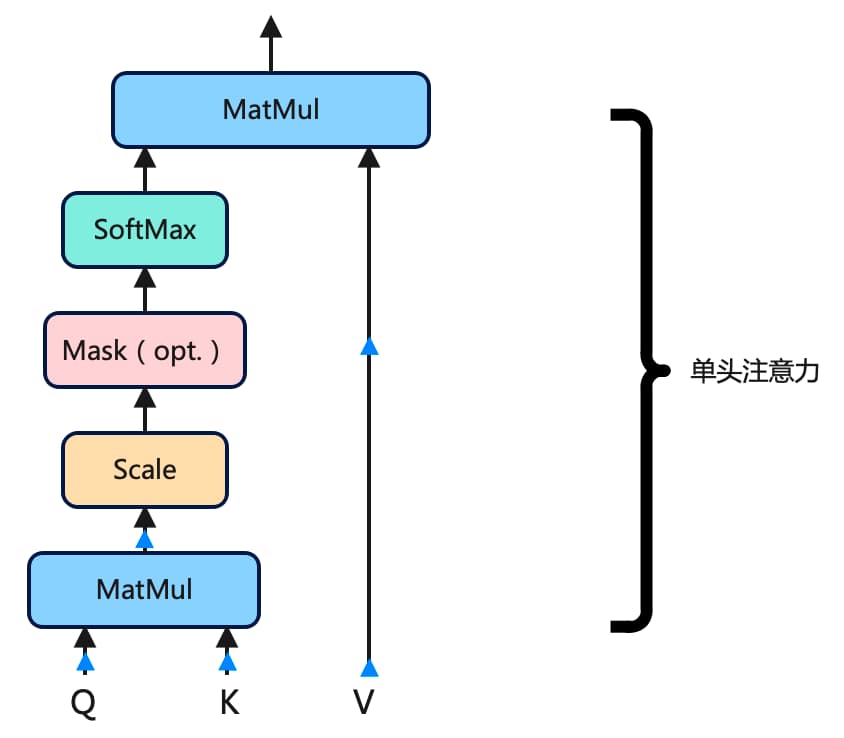
单头注意力机制在 Transformer 中有三个输入：查询Query、键Key和值Value。

QKV矩阵是通过将之前计算的相同矩阵的转置与词嵌入矩阵和位置嵌入矩阵相加，乘以不同的权重矩阵获得的。

假设，为了计算查询矩阵Query，权重矩阵的行数必须与转置矩阵的列数相同，而权重矩阵的列数可以是任意的；例如，我们假设权重矩阵中有4列。权重矩阵中的值是0和1之间随机数：

计算查询矩阵Query

使用相同的程序来计算键 和值 矩阵，但权重矩阵中的值必须对两者都不同。

在矩阵相乘后，得到的结果查询Query、键Key 和值Value 如下：

计算单头注意力

为了缩放结果矩阵，我们必须重复使用我们的嵌入向量（embedding vector）的维度，即6。

计算掩码

掩码就像告诉模型只关注某个点之前发生的事情，在确定句子中不同单词的重要性时不要窥视未来。它帮助模型以逐步的方式理解事物，而不会通过提前查看来作弊。

softmax

执行最终的乘法步骤以从单头注意力中获取结果矩阵。

在任何情况下，无论是单头注意力还是多头注意力，结果矩阵都需要再次通过乘以一组权重矩阵进行线性变换。

多个单头注意力

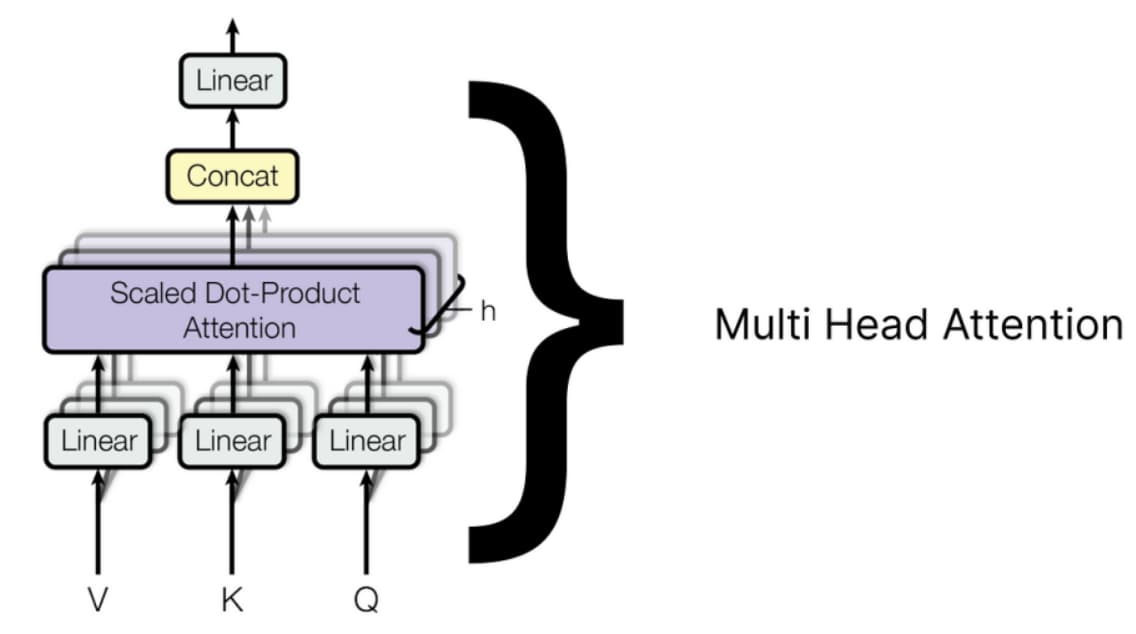
每个单头注意力有三个输入：查询、键和值，每个都有不同的权重集。一旦所有单头注意力输出它们的结果矩阵，它们将被连接起来，最终的连接矩阵再次通过乘以一组随机初始化的权重矩阵进行线性变换，这些权重矩阵将在 transformer 开始训练时进行更新。

Step8-添加层归一化

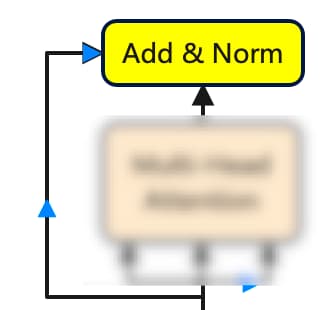
当从多头注意力中获取到结果矩阵后，接下来就是将其添加到原始矩阵中。为了规范化上述矩阵，计算每行的均值和标准差，并用矩阵中每个值减去对应行的平均值，然后除以对应的标准差。其中添加一个小的误差值可以防止分母为零，从而避免使整个项趋于无穷大。

Step9-前馈网络（Feed Network）

在将矩阵归一化后，它将通过前馈网络进行处理。我们将使用一个非常基本的网络，该网络只包含一个线性层和一个 ReLU 激活函数层。

首先，通过将最后计算的矩阵与一组随机的权重矩阵相乘来计算线性层，该权重矩阵在 transformer 开始学习时将更新，并将结果矩阵添加到一个也包含随机值的偏置矩阵中。在计算线性层之后，将其通过 ReLU 层并使用公式计算。

Step10-再次添加层归一化

从前馈网络获得结果矩阵，我们必须将其添加到从先前添加和归一化步骤获得的矩阵中，然后使用行均值和标准差对其进行归一化。该加法和归一化步骤的输出矩阵将作为解码器部分中存在的多头注意力机制之一的查询和键矩阵，可以通过从加法和归一化追踪到解码器部分来轻松理解。

Step11-解码器

在训练时，解码器有两个输入。一个是来自编码器，其中最后一个加和归一化层的输出矩阵作为查询和键，用于解码器部分的第二个多头注意力层。

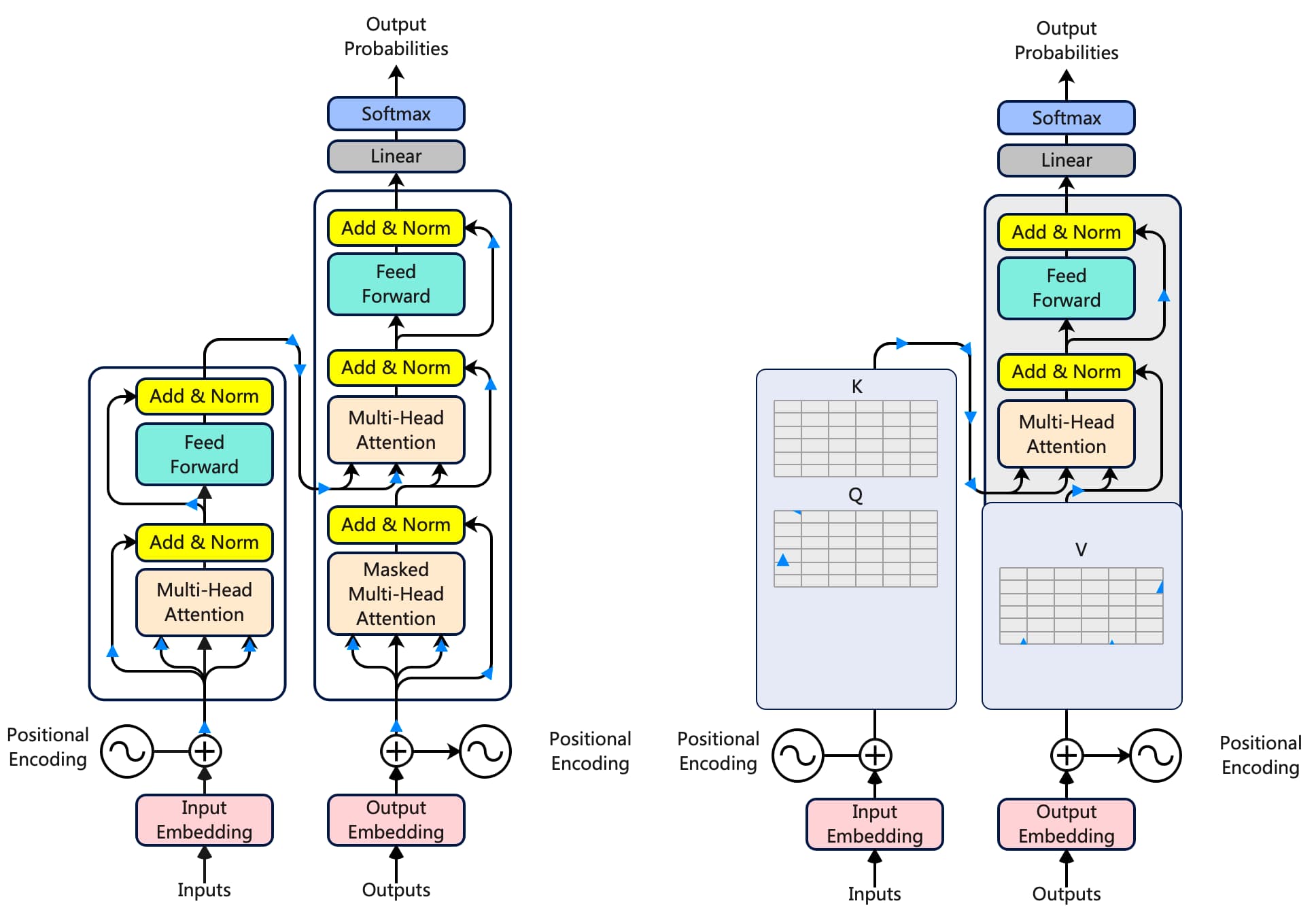
当值矩阵来自解码器在第一次添加和归一化 步骤之后。解码器的第二个输入是预测的文本。如果你还记得，我们输入到编码器的是马无夜草不肥，所以解码器的输入是预测的文本，在我们的例子中是人无横财不富。。

预测输入文本需要遵循一个标准的令牌包装，使 transformer 知道从哪里开始和在哪里结束。

在哪里<start> 和<end> 是两个新标记被引入。此外，解码器每次只接受一个标记作为输入。这意味着<start> 将作为输入，而人 必须是它的预测文本。

Step12-计算预测单词

输出矩阵必须包含与输入矩阵相同的行数，而列数可以是任何数量。解码器的最后一个添加和归一化块的结果矩阵必须展平，以便与线性层匹配，以找到我们数据集（语料库）中每个独特单词的预测概率。

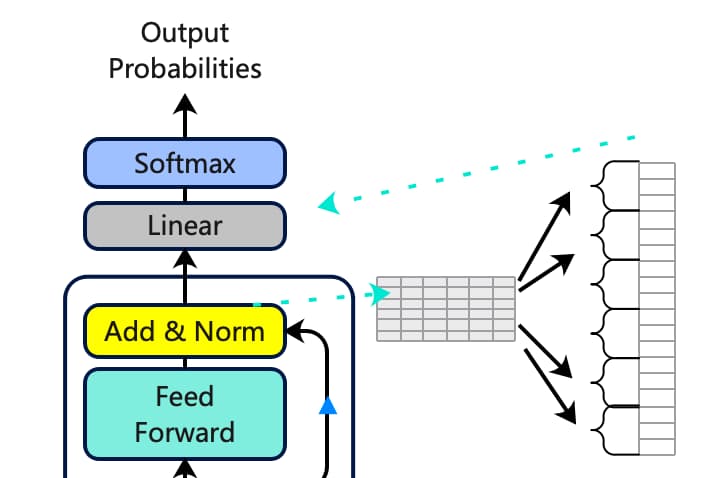
这个展平层将通过一个线性层传递，以计算数据集中每个独特单词的logits（得分），之后就可以使用softmax 函数对它们进行归一化，并找到包含最高概率的单词。